2D bimodal example

This example shows how to use lightkde.kde_2d and how it compares to scipy.stats.gaussian_kde for a bimodal bivariate case.

Import packages:

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde, multivariate_normal

from lightkde import kde_2d

Generate synthetic data from two univariate normal distributions:

np.random.seed(42)
sample = np.vstack(
    (
        multivariate_normal.rvs(mean=[0, 0], cov=0.3, size=2000),
        multivariate_normal.rvs(
            mean=[2, 2], cov=[[0.5, -0.48], [-0.48, 0.5]], size=2000
        ),
    )
)

Estimate kernel density using lightkde:

density_mx, x_mx, y_mx = kde_2d(sample_mx=sample)

Estimate kernel density using scipy:

gkde = gaussian_kde(dataset=sample.T)
xy_mx = np.hstack((x_mx.reshape(-1, 1), y_mx.reshape(-1, 1)))
scipy_density_mx = gkde.evaluate(xy_mx.T).reshape(x_mx.shape)

Plot the data against the kernel density estimates:

# pre-process
bins = (30, 30)
data_density_mx, xedges, yedges = np.histogram2d(
    sample[:, 0], sample[:, 1], bins=bins, density=True
)
z_min = 0
z_max = np.max(data_density_mx)
x_min, x_max = min(xedges), max(xedges)
y_min, y_max = min(yedges), max(yedges)

# plot
cmap = "afmhot_r"
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(10, 3), sharex="all", sharey="all")

# data
h = ax1.hist2d(
    sample[:, 0],
    sample[:, 1],
    bins=bins,
    density=True,
    vmin=z_min,
    vmax=z_max,
    cmap=cmap,
)[-1]
ax1.set_title("data")

# lightkde
ax2.contourf(x_mx, y_mx, density_mx, levels=50, vmin=z_min, vmax=z_max, cmap=cmap)
ax2.set_title("lightkde")

# scipy
ax3.contourf(x_mx, y_mx, scipy_density_mx, levels=50, vmin=z_min, vmax=z_max, cmap=cmap)
ax3.set_xlim(x_min, x_max)
ax3.set_ylim(y_min, y_max)
ax3.set_title("scipy.stats.gaussian_kde")

fig.subplots_adjust(right=0.89)
cbar_ax = fig.add_axes([0.90, 0.15, 0.05, 0.7], aspect=30)
fig.colorbar(h, cax=cbar_ax, label="density")
plt.show()

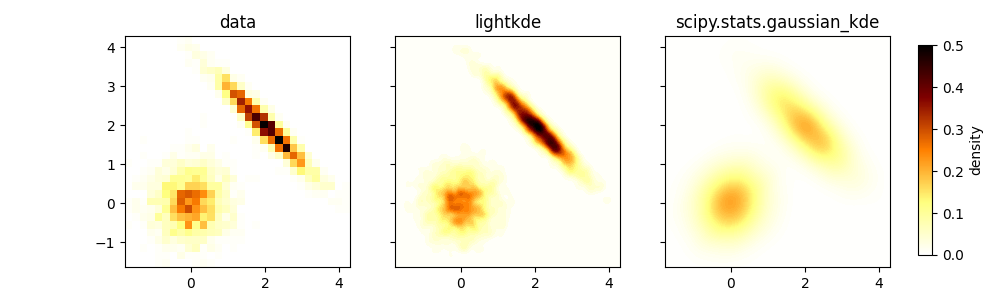
The scipy method oversmooths the kernel density and it is far from the histogram of the data that it is expected to follow.